Java를 사용하여 개발을 하기 위해서는 JDK, JRE, JVM을 필요로 한다.
오늘은 이것들이 무엇이며, 우리가 프로그램을 개발하고 실행되기까지 어떤 일들이 벌어지는지 알아보도록 하겠다.
1. JDK( Java Deployment Kit )
가장 먼저 알아볼 것은 자바 개발 도구이다.
JDK는 기본적으로 우리가 자바를 사용하여 개발하고, 실행하기 위해 필요한 것들이 담겨있다.
자바로 개발된 프로그램을 실행하기 위한 JRE와 필수적 그리고 기본적인 자바 개발 도구들(Java, Javac,...)등이 포함된다.
그럼 JDK만 설치되어 있다면 메모장만 사용해도 코드가 돌아가게 할 수 있나요?
물론이다. 이를 증명하기 위해 메모장으로 코딩을 진행해 보겠다.
우선, 텍스트 파일에 기본적인 코딩을 해보았다.

이후 해당 파일을 Java컴파일러로 컴파일하기 위해. java파일로 변경해 준다.
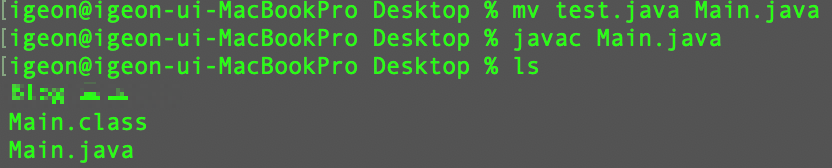
javac명령어를 사용하여 컴파일을 진행한다.
왜 컴파일을 진행해야 할까?
Java 코드는 사람이 읽기 쉬운 고급 언어이다.
이는 사람은 이해할 수 있지만 컴퓨터는 이해할 수 없는 언어라는 의미이다.
그럼 외국인과 대화를 하기 위해 번역가가 필요하듯이 언어도 번역가가 필요한데 이 역할을 수행하는 것이 컴파일러다.
또한 컴파일과정을 거치며, 문법적으로 잘못된 부분까지 체크를 진행하게 되고, 이때 발생하는 오류가 CompileException이다.
즉, 개발을 진행하면서 오류가 발생하였다면 문법이 잘못되었거나 실행할 수 없는 파일이라 보면 된다.
자바 컴파일러가 변환작업을 진행하면 자바 코드 소스를 바이트코드로 변환하게 되는데, 이때 확장자는. class고 이때서야 JVM이 해당 소스를 실행시킬 수 있다.

이후 java 명령어를 통해 Class를 실행시키면 정상적으로 작동하는 것을 확인해 볼 수 있다.
이렇듯 JDK를 설치한다면 단순한 text로도 개발이 가능한 것을 확인해 볼 수 있다.
2. JRE ( Java Runtime Environment )
우리가 만든 Java프로그램이 동작하려면, 단순히 컴파일을 거쳐. class파일을 만들었다고 실행되는 게 아니다.
실행을 하기 위한 머신, 라이브러리, 파일들이 필요한데, JRE는 이를 모아놓은 패키지이다.
위 글에서 보았듯 JRE는 JDK에 포함되어 있어 JDK를 설치하면 함께 설치된다.
( 버전에 따라 다르다. )
JRE은 다음과 같은 구성으로 이루어져 있다.
| 구성요소 | 설명 |
| JVM | 바이트코드를 읽어 실행하는 엔진 |
| Java 클래스 라이브러리 | 입출력, 네트워크, 컬렉션 등 기본 기능을 제공 |
| Java 클래스 로더 | 필요한 클래스를 메모리에 동적으로 로드 |
| 런타임 라이브러리 및 지원 파일 | JVM이 동작하는 데 필요한 추가 리소스 |
이를 보면 알 수 있지만, JVM은 이론적으로 JRE 없이 단독 설치하는 것은 어려우며, 실용적이지 않다.
왜냐면 JVM은 JRE의 일부분이며, JRE가 JVM이 작동할 때 필요한 기능들을 제공하기 때문이다.
3. JVM ( Java Virtual Machine )
자바 가상 엔진으로 Java로 작성된 프로그램을 실행시키고 관리하는 실질적인 주체입니다.
"JVM은 JRE 없이 사용하기 어려우면 JRE가 주체 아닌가요?"
위와 같은 의문이 들었다면 JRE가 무엇인지 다시 확인해 볼 필요가 있습니다.
JRE는 실행 환경 전체를 말하는 "패키지"고,
그 안에 포함된 JVM이 실제로 프로그램을 실행하고 메모리를 관리하는 주체로 이해하면 된다.
JVM은 운영체제에 영향을 받는데, 이 영향은 JVM에 한정적이기 때문에 Java 프로그램은 모든 플랫폼에서 제약 없이 동작할 수 있다.
이는 Java로 개발된 프로그램의 가장 큰 이점인데, Java로 작성된 코드는 컴파일 후 운영체제와 상호작용을 하는 것이 아닌 JVM과 상호작용을 하고, JVM이 운영체제와 상호작용을 하기 때문에 Java로 개발된 프로그램은 이식성이 좋다.

위 그림과 같이 컴파일된 바이트코드는 모든 JVM에서 동일하게 인식하기 때문에 운영체제에 맞는 JVM만 설치된다.
- 자바 컴파일러가. java를. class로 컴파일(바이트코드).
- JVM이 바이트코드를 바이너리코드로 변환.
- 변환된 바이너리코드를 CPU에서 실행.
여기까지가 간단하게 Java코드가 실행되기까지의 과정을 간단하게 다뤄보았다.
이제 내부적으로 어떤 일이 일어나는지 알아보도록 하자.
지금부터 알아볼 JVM의 구성요소이다.

- Class Loader
- Execution Engine
- JIT ( Just In Time )
- Interpreter
- Garbage Collector
- Runtime Data Area
- Method Area
- Heap
- PC Register
- JVM Stack
- Native Mathod Stack
3.1. Class Loader
클래스 로더는. class 파일을 메모리에 올려 런타임에 사용할 수 있게 만드는 역할을 한다.
- 클래스를 읽고( Loading )
- 검증하고 ( Verification )
- 필드와 메서드를 위한 메모리를 준비하고( Preparation )
- 심볼릭 참조를 직접 참조로 바꾸고 ( Resolution )
- 초기화 코드를 실행( Initialization )
여기까지 모든 클래스를 "사용 가능"하게 만드는 전체 파이프라인의 시작점이다.
이 작업들은 아래와 같이 3단계로 구분할 수 있다.
- Loading: 클래스 파일을 JVM의 메모리에 로드한다.
- Linking: 클래스 파일을 사용하기 위해 검증한다.
- Verifying: 읽은 클래스가 JVM에 명시된 대로 구성되어 있는지 검사한다.
- Preparing: 클래스가 필요로 하는 메모리를 할당한다.
- Resolving: 클래스의 상수 풀 내 모든 심볼릭 레퍼런스를 다이렉트 레퍼런스로 변경한다. - Initializing: 클래스 변수들을 적절한 값으로 초기화한다. (Static 블록 실행 및 필드 초기화)
용어정리
상수 풀( Constant Pool ): 클래스 파일에 있는 다양한 정보 저장소(클래스명, 메서드명, 필드 정보 등)
심볼릭 레퍼런스( Symbolic Reference ): "이 클래스/메서드/필드는 이름으로 이렇게 적혀있어요"라는 문자열 기반 정보
다이렉트 레퍼런스( Direct Reference): JVM 내부에서 사용하는 메모리 주소 또는 포인터
해당과정이 무작정 이뤄지지는 않는다.
JVM은 클래스를 “필요할 때” Load 하는데 이는 다음과 같은 이유가 존재한다.
- 메모리 효율성
- 애플리케이션 실행 시작 시간 단축
- 모듈화의 유연성 확보
즉, 처음에 모두 메모리에 적재할 경우 비효율성과 유연성을 떨어트리기 때문에 애플리케이션에서 필요로 할 때 메모리에 적재한다.
3.2. Execution Engine
실행엔진은 바이트코드를 해석하고, CPU가 이해할 수 있는 바이너리코드로 변환하여 실행한다.
변환하고 실행할 때 실행엔진은 코드를 실행하기 위해 Interpretr와 JIT을 사용한다.
3.2.1. Interpreter
- 바이트코드 명령어를 하나씩 읽어 해석하고 실행한다.
3.2.2 JIT Compiler
- Interpreter의 중복코드 중복 해석 및 실행에 대응하고자 도입.
- 바이트코드 전체를 컴파일하여 NativeCode로 변경.
- NativeCode로 변경한 바이트코드는 Interpreting 되지 않고 캐싱해 두었다 NativeCode로 직접 실행
NativeCode는 C나 C++, 어셈블리어로 구성된 인터프리터언어를 의미한다. - 중복 코드 실행의 경우 계속 Interpreting 하는 것보다 성능이 좋지만, NativeCode로 변경하는데 자원이 소모되기 때문에 Interpreter방식으로 사용하다 일정 기준이 넘어가면 JIT Compile방식 사용.
3.2.3 Garbage Collector
JVM은 Heap 메모리 영역에서 더 이상 참조되지 않는 메모리를 회수하기 위해 Garbage Collecor를 사용한다.
개발자가 직접 사용하는 것이 아닌 자동으로 작동하기 때문에 더욱 손쉽게 메모리 관리를 할 수 있다.
더 이상 사용하지 않는 데이터의 경우 null로 초기화해 주면, 더욱 효율적으로 Garbage Collector를 이용할 수 있다.
Garbage Collector는 주기적으로 작동하는 프로세스로서 참조되지 않는 메모리가 언제 해제되는지 알 수 없으며, GC가 작동하게 되면 GC관련 Thread를 제외한 다른 Thread들이 중지되기 때문에 오버헤드가 발생한다.
STW( Stop The World ): GC를 수행하기 위해 JVM이 프로그램 실행을 멈추는 현상
3.3. Runtime Data Area

Runtime Data Area는 JVM 메모리 영역으로 자바 프로그램을 실행할 때 사용되는 데이터를 사용 목적에 맞춰 나누어져 있다.
아래와 같이 크게 2가지 특징으로 분리를 해볼 수 있다.
- Thread-specific ( Thread마다 개별로 존재 )
- PC Register
- Stack
- Native Method Stack
- Shared (모든 Thread가 공유)
- Heap
- Method Area
Thread-specific은 Thread마다 개별로 존재하여 각 Thread 간 메모리 공유가 불가능하다.
Shared는 Thread와 별개로 할당된 메모리 영역으로 각 Thread들이 해당 메모리에 접근한다면 동일한 데이터를 사용할 수 있다.
3.3.1. PC Register
우리가 JVM의 PC Register를 이해하기 위해서는 CPU의 PC Register와 무엇이 다른지 이해해야 한다.
CPU의 PC Register는 현재 CPU가 실행할 다음 명령어의 주소를 저장하는 하드웨어 레벨 Register이다.
하지만 JVM의 PC Register는 물리적인 레지스터가 아니라 가상 머신 레벨에서의 명령어 실행 흐름 제어 구조이다.
그럼 왜 필요할까?
JVM이 바이트코드를 실행할 때 다음 구조를 따른다.
[바이트코드] → [PC Register (현재 위치)] → [Opcode 해석기] → [Operand Stack]
아래 코드를 사용하여 한스탭씩 따라가 보자.
int a = 1 + 2;코드를 바이트코드로 컴파일하면 아래와 같은 결과물이 나온다.
iconst_1
iconst_2
iadd
istore_1해당 코드를 실행한다면 PC Register는 iconst_1의 위치를 가르치고,
순차적으로 프로그램의 흐름을 추적한다.
그럼 PC Register가 가리키는 바이트코드를 Interpreter가 읽어 해당 명령에 대응되는 C/C++ 함수를 실행한다.
이후 Interpreter가 실행한 C/C++함수가 CPU를 작동시키게 된다.
이렇듯 Java는 CPU에게 바로 연산시키는 것이 아닌 현재 실행해야 하는 연산을 제공하여야 하며, 이를 위한 버퍼 공간으로 사용하기 위해 PC Register메모리 영역이 존재한다.
또한 PC Register는 Thread마다 각각 가지고 있다.
즉, "현재 Thread의 어떤 명령어가 실행 중인가?"에 대한 명령어 주소를 기억하고 있다.
3.3.2. Stack
스택은 원시타입( Primitive type ) 데이터와 참조타입(Reference type)의 주소값, 현재 실행 중인 메서드의 스택 프레임을 저장하는 메모리 영역이다.
LIFO구조로 push와 pop기능 방식으로 동작한다.
Thread마다 하나씩 존재하며, Thread가 시작될 때 할당되며, Thread가 종료되면 사라진다.
이때, 프로그램 실행 중 할당된 메모리를 벗어난 데이터들이 들어온다면 StackOverFlowError가 발생한다.
3.3.3. Native Method Stack
이는 실제 개발하면서 보기는 힘들고, 내부 라이브러리를 깊게 파보면 native선언을 해둔 것을 확인할 수 있다.
이는 Java로 구현된 것이 아닌 C/C++과 같은 언어로 구현되었다는 의미이며,
예시로 Thread Class를 보면 registerNatives 메서드는 native선언이 되어 있는 것을 확인할 수 있다.
public class Thread implements Runnable {
/* Make sure registerNatives is the first thing <clinit> does. */
private static native void registerNatives();
static {
registerNatives();
}
}그럼 왜 Java로 작성하지 않고 C/C++로 대신 구현하는 것일까?
- 시스템 리소스 접근
- 성능이 중요한 로직을 C/C++로 최적화
- 기존 C/C++ 라이브러리와 연동
그렇다 컴파일 언인 Java보다 인터프리터언어인 C/C++ 이 성능적으로 앞서 성능 최적화를 한다거나 시스템에 직접 접근하려 할 때 사용하는 것을 확인할 수 있다.
Native Method Stack을 통해 C함수 호출 프레임을 관리하여 JVM은 해당 기능을 사용할 수 있는 것이다.
3.3.4. Heap
힙영역은 참조타입( Reference type ) 데이터들이 저장되며, new연산자로 생성되는 Instance들이 저장된다.
해당 영역에 존재하는 데이터들은 Stack영역에서 참조하지 않으면 GC대상이 된다.
3.3.5. Method Area
흔히 Class와 Static으로 선언된 변수 혹은 메서드들이 프로그램이 시작될 때 메모리에 로드되어 프로그램이 종료될 때까지 남아 있다.
Heap과 동일하게 모든 Thread가 공유하고, 여러 정보들을 저장하고 있다.
- Field Info: 멤버 변수명, data type, 접근 제어자의 정보
- Method Info: 메서드명, return type, 매개변수, 접근 제어자
- Type Info: Class인지 Interface인지 저장, Type의 속성, Super Class의 이름
즉, 정적 필드와 클래스 구조만을 가지고 있다.(클래스는 new로 생성할 경우 Instance가 Heap에 생성된다.)
3.3.6. JNI
Java Native Interface로 다른 언어로 만들어진 애플리케이션과 상호 작용할 수 있는 인터페이스를 제공한다.
3.3.7. Native Method Library
C/C++로 작성된 라이브러리다.
자바에서 native 키워드로 선언된 메서드를 호출할 때, 필요에 따라 JNI를 통해 해당 네이티브 라이브러리를 호출하며, 이 과정에서 Native Method Stack이 사용된다.
4. 글을 마치며
JVM, JDK, JRE에 어떤 것들이 존재하고, 어떤 역할을 하는지에 대해 알아보았다.
이전부터 알고 있던 내용들도 있었지만, 시간을 충분히 투자하며 차근차근 공부해 보니 확실히 모르고 있었던 부분도 많이 보였던 거 같다.
"Java개발자가 JVM을 이렇게까지 알아야 하나요? 그냥 코드 잘 짜면 잘 돌아가잖아요."
어느 정도 맞는 말인 거 같다.
JVM내부 요소들을 건드리며 개발을 안 하더라도 서버 스펙만 좋다면 아무런 문제 없이 돌아갈 것이다.
개판으로 작성해도 잘 돌아갈 텐데 잘 짰으면 얼마나 잘 돌아갈까.
하지만 알고 있다면 메모리를 좀 더 신중하게 사용할 수 있을 것이고, 성능적으로 한 번쯤은 고민해보지 않을까?
그리고 어떤 문제가 발생했다면 이를 해결하기 위해 고민을 할 때 이러한 공부들은 많은 도움이 될 것이다.
그리고 도구를 사용하면 어떤 도구인지 알고 있으면 잘 사용하지 않겠나.
References
https://d2.naver.com/helloworld/1230
'Java' 카테고리의 다른 글
| 제네릭과 오버로딩: 왜 "B0"이 출력될까? (1) | 2025.02.11 |
|---|---|
| [ThreadLocal] Thread영역에 데이터를 저장하고 싶어요 (1) | 2025.01.27 |
| 오차 없는 실수 연산 어떻게 해야 할까? (0) | 2025.01.10 |
| [Java] Static (3) | 2024.12.26 |
| [ Basic ] I/O Stream이란? (0) | 2024.12.23 |